Comparing Fractions with Playing Cards

We are knee deep in our study of fractions in my 4th grade math class right now. Fractions are my ultimate favorite concept to teach. I actually get giddy when I know my fractions unit is coming up
because I LOOOOOVE seeing what their understandings are and figuring out ways to illicit the depth of their knowledge. Over the years, I've learned to break the concepts down and really figure out how to scaffold from one level of understanding to the next. {Looking back at your previous grade level's standards and forward to the next grade level's standards is a great way to gain an understanding of the depth of knowledge expected and to figure out how to drop back some or increase the rigor a bit.}
After a few introductory activities to get my fractions unit going {imagine lots of playing with manipulatives, making our own fractions out of paper, and finding equivalents}, I scoured pinterest to find new ideas {I added my findings to my Everything Fractions Pinterest board}. I'm sure you've seen many opportunities to use playing cards in math, and I came across one for fractions that jogged my memory and I just knew I had to break this game out immediately. {Mrs. Wilson's Easy Math Centers with Dice and Playing Cards for 5th Grade resource is on my wishlist!}

The Image I Saw from Mrs. Wilson's Wolves
I had already introduced comparing fractions with my Comparing Fractions Task Cards. Using these cards, I explained 4 strategies we can use to think through fraction comparisons:
1} If the numerators are the same, look at the denominator. The smaller denominator has pieces that are larger, so it is the larger fraction.
2} If the denominators are the same, the greater fraction is the one with more pieces (larger numerator).
3} Use Fraction Benchmarks: Think about less than 1/2, equal to 1/2, greater than 1/2.
4} If 1, 2, and 3 don't work, find Common Denominators to compare. {This is where it gets tricky because their fraction understanding of this is not there yet.}
Students also brought up that if both fractions are 1 away from 1 whole, you can think about the size of the pieces.
Although I used these cards to introduce comparing fractions, I decided to step back and have my students learn the concepts sheerly through game play for a few days. As I changed the game up each day, I also found ways to make them WANT to learn what I needed to teach them.

On day one, I gave partners a set of playing cards. I ran around to each desk and drew fraction bars and a circle on their desk with an expo marker. I've read that some teachers take out the face cards, but I left everything in. We talked about King, Queens, and Jacks being a 10 and Aces being an 11.
I made a simple recording sheet for them to write down their fraction comparisons.
When my kiddos play a game together, I nearly always have them record their rounds. This way, I can pop around and look at past rounds and see if anyone is off track.
For this fraction game, it was really helpful to have them go back and investigate fractions that were close calls and really needed common denominators to prove which fraction was larger. I feel so guilty sometimes asking students to record info when playing a game, but they happily chose one person to be the recorder and didn't seem to mind at all.
During our first day of game play, I did not set any rules. Students turned over their top two cards and made a fraction. I just wanted to see how much they had already internalized about using fraction benchmarks and understanding how to compare the size of the pieces by thinking about the denominators.
At the end of this game session, I pulled everyone together and asked what kinds of cards they hoped to get. Most everyone had figured out that 11/2 was the greatest fraction they could create. I also wanted them to generalize that creating improper fractions almost assured them a win. Students verbalized that they wanted to flip over a fraction that had a numerator larger than the denominator. Yes!
Now, as I watched them play with no rules, my brain was already spinning with ways to increase the rigor and force them to use more fraction understandings.

On day two, I made a "no improper fractions or whole numbers" rule. Students had to create fractions less than 1 and had to tap into strategies like comparing to 1/2 and looking at the size of the denominator. In some cases, students really needed to use a common denominator. This is where I stepped in with my expo marker and began teaching individual students how to find common denominators during their game play. {Much more effective and engaging than just watching me explain it at the whiteboard!}
During this round 2 game play, I found that by eliminating improper fractions and whole numbers, misconceptions where students used their "feelings" to decide which fraction was larger abounded. For example, I heard a lot of "2/3 is only 1 away from 1 whole. 7/9 is 2 away from 1 whole, so 2/3 must be larger." I used common denominators to help students see that when two fractions are really close together, this logic does not work. I also had students realize that they could use logic like "Well, 3 x 3 is 9, but 3 x 2 only gets you to 6, so 7/9 is larger." Fortunately, the recording sheet allowed me to catch some of the closer fraction comparisons as I popped from partnership to partnership. Even if students were correct, I questioned them about how they decided which fraction was larger. I often worked out the common denominator comparisons to begin planting the seeds for that skill.
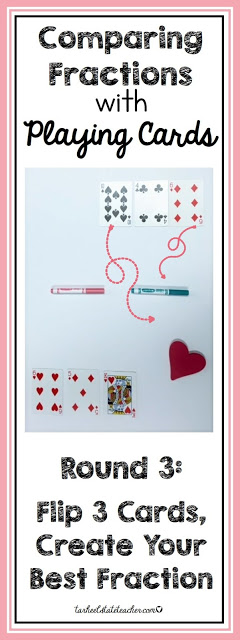
As I watched students play that day, a way to increase the rigor and make them think even more popped into my head. For round 3, students flipped over three cards and used them to make their best possible fraction. For each round, students simply kept the card they did not use and flipped over two more to continue game play. (Improper and whole numbers were still not allowed). It really required some critical thinking to figure out what cards would create the fraction that was closest to 1 whole and then to compare that fraction to their partner's fraction.
You can see in the image to the left that the top player would play 4/6 and the bottom player should play 5/6. My students would most likely use the understanding that 4/6 is a little more than 1/2 while 5/6 is closer to 1 whole to compare these fractions.
As I watched students choose their greatest possible fraction from the 3 cards they flipped, I could see which students were really gaining an understanding of the size of fractions.
In the case of a draw for any of our rounds, my students played a second round and the winner of that round got all of the cards. Also, I just realized that an Ace could be played as a 1 or 11. Using it as a 1 would have allowed my students the opportunity to compare unit fractions, so this is something I will try in the future.
When we return from spring break, we will be working on converting mixed numbers and improper fractions. We can play our card game again with the rule that students may only create improper fractions. With this stipulation,
I can use the game to teach them how to turn improper fractions into mixed numbers and then compare to one another.
There are so many ways to keep changing up this simple card game concept to increase the rigor and to guide students to focus on new concepts that you need to teach them.
It makes my heart so happy when students are working in partners, having fun, and having mathematical dialogue. I LOOOOVE to listen for deep understandings and misconceptions to help guide my teaching. Students asked me each day if they would get to play the comparing game again. A sure sign that they had fun and loved it! After all of our rounds, we returned to my Comparing Fractions Task cards. They worked individually, and most students zipped right through. Because of all the time we had spent learning through game play, I was able to target the few students who were still having a little difficulty solidifying their understandings.
I LOVE using games, dice, task cards, and other hands-on math strategies. Click the image for more of my Math Hacks and stay tuned because I have a year's worth of math hacks I haven't had a chance to share yet!
What other ideas do you have for using playing cards with fractions? I'd love to hear in the comments!




