How to Teach Area Model Division
I am absolutely in love with teaching whole number division through the area model or the rectangular array model (which I’ve also called the “box method” and the “rectangle method” for division).
I’ve found that the area model for division is usually taught one of two ways—in one approach, students are taught that they MUST use the largest partial quotient for each place of the dividend. In the second approach, students can begin with any number that makes sense to them and they are not required to always take the largest amount possible from the dividend. This approach is more “open-ended” and this is the way that I teach the area/rectangular array model to my students.
Having a method for division that allows for multiple entry points for students is why I love this method so much and one of the main ways it differs from the rigidity of the standard algorithm for division.
I do, however, encourage students to find more efficient ways to divide (use larger partial quotients/multiples of the divisor) as we move through our unit, so that they do not have to go through as many subtraction steps to get to the answer AND so that they learn to be thoughtful in the partial quotients that they choose.
Efficiency with the area model is something I think students can develop with encouragement and experience, but not something that I think needs to be required in teaching this method for division right at the beginning of students’ learning.
Four Benefits of Teaching with the Area Model/Rectangular Array Model for Division
-The Area Model for Division provides entry points for all students to begin solving larger division problems, regardless of their multiplication fact knowledge (when taught the “open-ended” way).
-Using and explaining the “boxes” for the area/rectangular division model allows students to connect division to “taking away” from what we have to create as many “equal groups” as possible. (In my teaching, the rectangles serve as a symbolic representation of an actual box or group of something.)
-Students can check their work using the same exact division method, but beginning with a different starting number.
-Students can be encouraged to solve the problem “another way” to develop their understanding of the model and become more efficient. (When solving example problems in whole group or small groups, I ask students who have “solved” the division problem if they can solve it another way using the same method.)
My Introduction Lesson for the Area/Rectangular Array Model for Division
In my first lesson to introduce the area model for division to students, I grab a Scholastic Book Order box and a sheet of colored copy paper. On the colored copy paper, I write a 3 digit dividend and “books.” (If you are teaching 5th grade, you can be brave and use a number in the 1,000s).
Let’s use 989 books shared among 6 teachers as our example. I tell students something like this:
We just received a huge shipment of books for 6 teachers to share. Pretend they all fit in this box (holding up the Scholastic box). Won’t the teachers be so excited to get their hands on these new books?!
It’s our job to figure out how many books each teacher will get! How would you start to “divide out” these books?
Individual whiteboards are a great addition to this lesson because you can get ideas from each student and see what they are thinking. I prompt students to jot down a number of books that they think we can give 6 teachers without running out. I tell them we don’t have to figure out the EXACT number the teachers will get. We just want to deliver some books to each classroom without running out.
I also usually make a big “to do” about how we could totally give the teachers one book at a time until we run out (I kind of run around the room pretending to give out one book at a time from the box). I ask students what they think about that and comment that it would take a long time, and wouldn’t be very efficient.
After students have had a chance to jot down a number for an idea, I have them show me their whiteboards and I write down 5-10 of their ideas on the whiteboard.
100 to each teacher- S- “100 is a big portion of the books we have to give away;” T- How do you know you won’t run out of books? “6 x 100 is 600.”
10 to each teacher- S- “10 x 6 is 60.” T-And then, could you give away 10 to each teacher again? What do you think about using 10? S “Yes. We could give 10 to each teacher a bunch of times, but I think 10 would take a long time.”
50 to each teacher- S- “50 x 6 is 300. 50 would be a good number because the teachers can carry them more easily. It wouldn’t take as long to give the books away as 10 at a time would.” T-Could you give each teacher 50 books again? S-“Yes. Then that would be 600 books given away.” T-Could you give each teacher 50 books a third time? S-“Yes. That would be 900 books given away.”
After you have analyzed a few of these options with your students whole group, you can have them turn and talk with a partner to discuss the number of books they thought they could start with (written on their whiteboards).
Now it’s time to progress to next steps.
Let’s keep going with Student 3’s idea to share 50 books at a time among the 6 teachers.
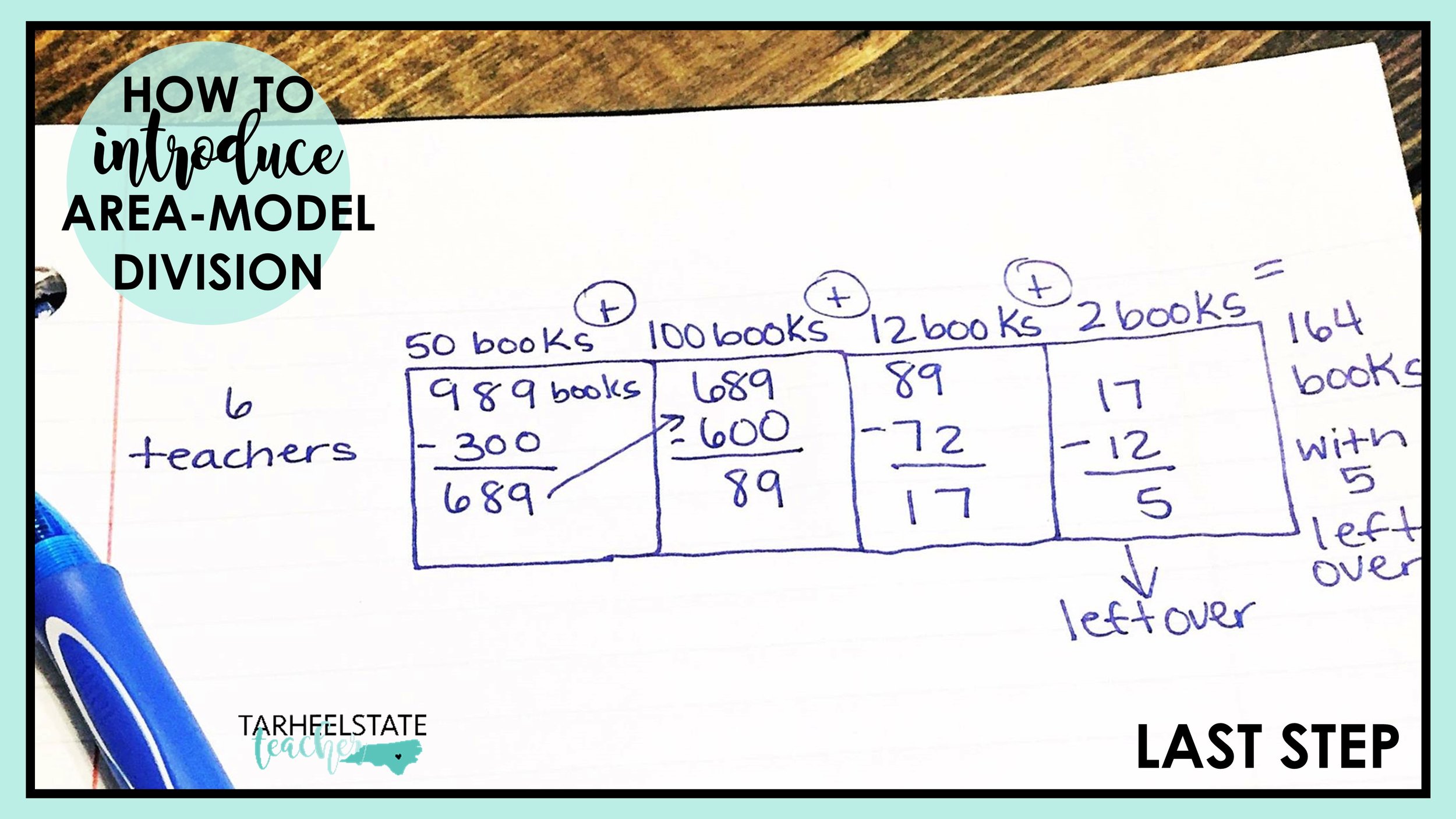
1) Draw a rectangle on the whiteboard. Write 989 inside the top of the rectangle. Explain to students that the rectangle represents your Scholastic box and 989 is the number of books you have to share among the teachers.
2) Write 6 to the left of the box. Ask students what the 6 represents. (The number of teachers to share the books—you can write “6 teachers” to the left of the box to give the divisor a label).
3) “So, if we give each teacher 50 books (write 50 books above the rectangle—I do like to use labels during the beginning of this learning process), how many books would we give away in total?”
4) Students should tell you that you will have given 300 books away. “Now, I’m going to subtract those 300 books from the 989 books we started with to see how many books we have left to share. That’s 689 books left to give to the teachers. I’ll create a new “box” that’s clean so that I can work out how many more books I can give the teachers. Now, we want to give the teachers ALL of the books we possibly can, right. Can we give them 50 books again?”
At this point, students should say that yes, you can give away 50 books to each teacher again. Perhaps a student will recognize that you could give away 100 books to each teacher now since you are left with 600. If students do not realize or share this idea, you could go ahead and “share” 50 books per teacher OR you could prompt them to see if there is a bigger number that can be given to the teachers. Don’t spend too much time allowing students to search for a bigger number—this will slow them down on being able to catch on to the rectangle method.
5) Let’s assume students want to go ahead and give each teacher 100 books in the next step. “Now, if we give each teacher 100 books, how many books have we delivered? 600. I’ll subtract 600 from 689. And we are left with just 89 more books to share among the teachers. I’m going to note above this rectangle that we gave 100 books to each teacher in our second round of delivering them.”
6) “Now that we have 89 books left, how many books can we deliver to each teacher without running out?” (This is another great time to have students show you what they think on their whiteboards. You may get a range of answers like 10, 11, 12. If a student shows you a number less than 10, you can ask them if they could go larger, just to push them a bit to be more efficient. I’d go with 10, 11, or 12 to get a move on with this problem during the lesson). “I see quite a few mathematicians who would like to give 12 books to each teacher. Let’s use 12 and see what happens next. If we give each teacher 12 books, how many books will we have delivered in our third delivery? 72. I’ll write 12 books above our third rectangle. When we subtract 72, how many books do we have left to share? 17.”
7) “Now, we have 17 books left to give away. How many can each teacher get?” Each teacher can get 2 more books. “Ok, I’ll write + 2 books above our fourth rectangle. When we give away 2 books to each teacher, how many books will we have given away? 12. And, how many books will we have left over?” 5 books left over. “Yes. We’ll have 5 books left over. We will have to let the teachers decide what to do with those 5 books, but for now, let’s call them leftovers.”
8) “The last thing we should do is figure out how many books each teacher gets in total. How would we figure that out?” Hopefully students realize that you need to add each portion of the books that have been given away to get a total. “Yes, we will add 50 + 100 + 12 + 2. Each teacher received 164 books and 5 books were left over.”
9) After finding the answer to this problem, I’d go through all of the steps again with the same division situation, but choose another starting point from the original ideas that students had. This will show students that they can start the problem in a variety of ways (whatever initially makes sense to them), and that it is possible to do so while finding the same quotient.
One tip/strategy that I’ve found useful is to have students create a “cheat sheet” of multiples of the divisor before starting the problem—and especially if they cannot quickly come up with multiplication facts for the divisor based on their multiplication fact knowledge. (You may want to call this an “easy fact” sheet or a “help sheet” if you do not want to call it a “cheat sheet.” I just explain to students that it’s not really cheating when it comes out of your own head.)
I encourage my students to use “easy” multiplication facts to begin “taking away” from the dividend. Rather than spending tons of time adding up multiples (mentally or on paper) or trying to get as close as possible to the dividend, students use the facts that come easiest to them and just get moving.
The area model allows us to break the dividend into manageable chunks, “take away” the amount that makes sense to us, and keep moving. I regularly explain to my students that if they just get started in the first block (partial quotient), the next block will be easier.
Some example “cheat sheet” numbers for our example problem would be:
6 x 10 = 60
6 x 100 = 600
6 x 5 = 30
6 x 50 = 300
6 x 11 = 66
6 x 110 = 660
Given this “cheat sheet” list, you can also see the variety of entry points that students can start with. I encourage you to expect students to complete division problems with the area model following through at least 2 different starting points for the problem; you can get them to “buy in” to solving the same problem again by telling them that this is a great way to check their work.
I’ve created a set of free division task cards that you can use to give your students “real-world” context for division problems. I’ve used the “box” concept with various school supply items as the quotients. I’ve also included two versions of the card—one set has the 1-digit divisor stated, while the second set is made so that students can roll a dice and come up with numerous divisors for the problems given.
Check them out in the photo and just drop your email to have these sent to your inbox!
NOTE: If you are already subscribed, just head to the free resource library and enter your password!